그래프(Graph)에 대해

 

https://www.tutorialspoint.com/data_structures_algorithms/graph_data_structure.htm

1. Graph 자료구조

• Graph란, 정점(node, vertex)과 정점 사이를 잇는 간선(edge, link)으로 구성된 자료구조이다
• 객체와 객체 사이의 관계를 나타내는데 좋은 자료구조로, 지하철 노선도, 비행기의 항로, 도로 등 다양하게 응용 가능하다

 

2. Graph의 구성

• 정점 : Graph에 속한 객체 (노선도의 경우 각 역)
• 간선 : 정점 사이의 관계를 나타내는 선 (두 역 사이에 지하철이 다니면 선이 존재하지만, 다니지 않으면 존재하지 않는다)
• 차수 : 정점에 연결된 간선의 갯수 (신촌역은 차수가 2이지만, 왕십리역은 차수가 6이다)
• 입력 차수(진입 차수) : 방향 그래프의 경우, 정점으로 들어오는 간선의 갯수
• 출력 차수(진출 차수) : 방향 그래프의 경우, 정점에서 나가는 간선의 갯수
• 사이클 : 어떠한 정점 A에서 간선을 한번씩만 이동했을때, 자기 자신으로 돌아오게 되는 경로, 또는 그러한 그래프
• 인접 정점 : 어떤 정점 A에서 간선으로 직접 연결된 정점

 

3. Graph의 종류

무방향그래프 / 방향그래프

• 무방향그래프

  

  https://mathinsight.org/definition/undirected_graph

  • 간선에 진행 방향이 없는 그래프, 양 방향 이동이 자유롭다
  • A->B 간선은 B->A간선과 동일하다
  • ex) 지하철

 

• 방향그래프

  

  https://mathinsight.org/definition/directed_graph

  • 간선에 진행 방향이 있는 그래프, 해당 방향으로만 진행 가능
  • A->B간선만 존재하면, B에서 A로는 이동할 수 없다
  • ex) 일방통행 도로

 

완전그래프 / 부분그래프

• 완전그래프 

  

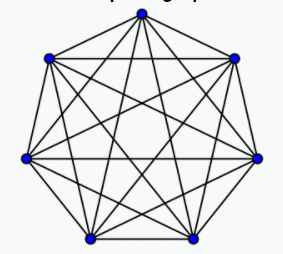
  https://en.wikipedia.org/wiki/Complete_graph

  • 모든 정점 사이에 간선이 연결된 그래프
  • 간선의 갯수는 n(n-1)/2이다 (무방향 기준)

 

• 부분그래프
  • 완전그래프가 아닌 그래프
  • 간선으로 직접 연결되지 않은 정점들이 존재한다

 

가중치그래프

• 가중치그래프

  

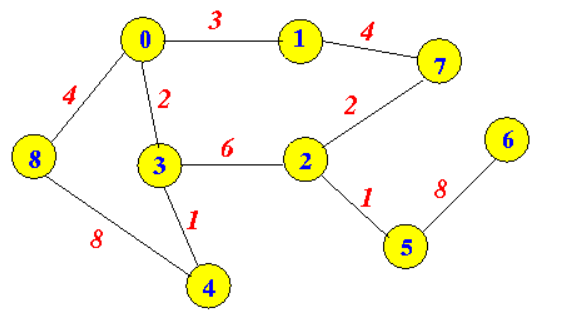
  http://www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/weighted.html

  • 간선에 각각 가중치 value가 부여된 그래프
  • ex) 지하철의 요금, 도로의 거리 등

 

4. Graph의 저장 방법

인접 행렬 / 인접 리스트

• 인접 행렬
  • N개의 정점이 있다면, N*N 2차원 배열으로 연결 정보를 관리한다
  • adj[i][j]는 i->j로 가는 간선의 유/무 혹은 그 갯수를 저장한다
  • 장점 : 특정 노드들 사이의 간선 존재 여부를 O(1)으로 확인 가능하다
  • 간선의 갯수가 많은 밀집 그래프에서 유리하다
  • 단점 : O(N^2) 크기의 배열이 필요하다

• 인접 리스트
  • 각 정점에 대해 리스트를 만들어, 인접한 정점정보만 저장한다
  • 간선이 없는 정점은 저장하지 않는다
  • 장점 : 실제 간선이 존재하는 경우만 저장하므로, 공간 복잡도가 낮아진다
  • 간선의 갯수가 적은 희소 그래프에서 유리하다
  • 단점 : 특정 노드들 사이의 간선 존재 여부를 확인하려면, 리스트를 탐색해야한다

간선 리스트

• 간선 리스트
  • 정점이 아닌, 모든 간선의 리스트를 저장한다

 

5. Graph 연관 알고리즘

Graph 탐색 (링크)

• DFS
• BFS

최소신장트리(Minimum Spanning Tree, MST) (링크)

• 그래프의 모든 정점을 잇는 간선의 가중치의 합이 최소가 되는 트리
• 크루스칼(KRUSKAL) 알고리즘
• 프림(PRIM) 알고리즘

최단경로 탐색

• 특정 정점에서 다른 정점들까지 가는 최소 가중치의 경로를 탐색
• 다익스트라(Dijkstra) 알고리즘
• 벨만-포드 알고리즘
• 플로이드-와샬 알고리즘