그래프부터 알아보기
https://vivadifferences.com/difference-between-dfs-and-bfs-in-artificial-intelligence/
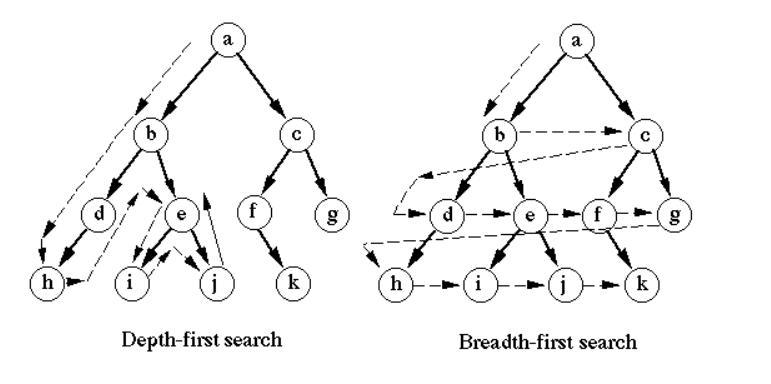
1. 너비 우선 탐색 (BFS)
- 현재 탐색 정점과 인접한 노드들을 우선 탐색한다
- A정점에서 시작했다면, A-B를 탐색한 후 B의 인접노드인 D/E가 아닌 C를 우선 탐색한다
- 시작 노드로부터 거리가 1인 모든 정점 탐색 - 거리가 2인 모든 정점 탐색 - 거리가 3인....
- 최단거리 찾기, A-B 사이 거리 찾기 등에 활용 가능하다
- FIFO 자료구조인 큐를 사용하여 구현한다
- A탐색 - B/C를 offer - B pop, 탐색 - D/E를 offer - C pop, 탐색 - .....
2. 깊이 우선 탐색 (DFS)
- 더 이상 깊이 갈수 없을때까지 우선 탐색하며, 탐색할 노드가 없으면 부모 노드로 돌아온다
- A정점에서 시작했다면, A-B를 탐색한 후 B의 인접노드인 D - D의 인접노드인 H ... 순서로 탐색한다
- 한 경로로 진행했을때 가능한 모든 경우의 수를 탐색한 후 다른 경로로 진행
- 경로별 특징이 나타나는 문제에 활용 가능하다
- LIFO 자료구조인 스택을 사용하거나, 재귀를 사용하여 구현한다
- A탐색 - C/B를 push - B pop, 탐색 - E/D를 push - D pop, 탐색 - .....
- A탐색 - B로 재귀 - B탐색 - D로 재귀 - .....
3. 각 방식의 특징
- DFS BFS 다 방문한 노드 / 방문하지 않는 노드를 구분할 수단이 필요하다
- 4번의 예시 코드는 별도의 Boolean 배열을 이용했으며, tree와 같은 특수한 형태의 graph는 부모-자식 관계를 이용하기도 한다
- 재귀를 사용한 DFS는 노드 방문 시점에서 방문처리를 해도 무방하다.
- 스택을 사용한 DFS / 큐를 사용하는 BFS의 경우 노드 방문 시점에서 방문처리를 하면 스택/큐에 노드가 중복 삽입된다
https://math.stackexchange.com/questions/1548708/finding-dfs-in-undirected-graph
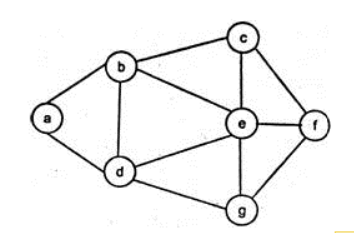
- ex)A에서 DFS를 한다면 B/D를 스택에 넣게되는데, B를 pop해 DFS를 할 때 D는 방문하지 않은 상태로 중복 삽입된다
- 때문에 실제 방문하는 시점이 아닌, 방문 예고 시점, 즉 스택/큐에 넣는 시점에서 방문처리를 해야 한다
- 모든 노드를 탐색하는 경우 DFS와 BFS의 차이는 거의 없지만, 다른 문제에서 응용하는 경우 DFS보단 BFS를 자주 사용한다
- DFS의 경우 해당 경로에 해답이 없고 깊이가 무한일 경우 탈출할 수 없게 된다
- 또한 다양한 해가 있을 경우 DFS의 경우 최초 발견한 해와 최소 깊이의 해가 같다고 말할 수 없지만,
- BFS의 경우 최초 발견한 해가 최소 깊이의 해가 된다. (최소 거리 문제에서 사용하는 이유)
- BFS는 특정 노드에 진입한 경로를 확인할 수 없지만
- (ex. 위 그래프에서 BFS로 e노드에 진입시, 그게 a-b-e인지 a-d-e인지 알 수 없다)
- DFS는 어떤 경로로 해당 노드에 진입하는지 확인하는게 용이하다
- (ex. DFS를 진행하며 거쳐온 node를 표시해 두면, 지금까지 지나온 노드 정보를 확인 가능하다)
4. JAVA 기초 코드 (DFS와BFS)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args)throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
sb = new StringBuilder();
graph = new ArrayList<ArrayList<Integer>>();
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int V = Integer.parseInt(st.nextToken());
for (int i = 0; i <= N; i++) {
graph.add(new ArrayList<Integer>());
}
//graph 입력
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int node1 = Integer.parseInt(st.nextToken());
int node2 = Integer.parseInt(st.nextToken());
graph.get(node1).add(node2);
graph.get(node2).add(node1);
}
//graph 정렬
for (int i = 0; i <= N; i++) {
graph.get(i).sort(null);
}
isChecked = new boolean[N+1];
DFS(V);
sb.append("\n");
isChecked = new boolean[N+1];
isChecked[V]=true;
BFS(V);
sb.append("\n");
System.out.println(sb);
}
static StringBuilder sb;
static ArrayList<ArrayList<Integer>> graph;
static boolean[] isChecked;
static void DFS(int i) {
sb.append(i).append(" ");
isChecked[i]=true;//방문처리
for (int j = 0, len = graph.get(i).size(); j < len; j++) {
int temp = graph.get(i).get(j);
if(!isChecked[temp]) {//이미 방문했던 노드는 재방문하지 않는다
DFS(temp);//재귀로 자식노드 우선처리
}
}
}
static void BFS(int i) {
Queue<Integer> q = new LinkedList<Integer>();
q.offer(i);
while(!q.isEmpty()) {
int next = q.poll();
sb.append(next).append(" ");
for (int j = 0, len = graph.get(next).size(); j < len; j++) {
int temp = graph.get(next).get(j);
if(!isChecked[temp]) {//이미 방문했던 노드는 재방문하지 않는다
isChecked[temp]=true;//방문처리
q.offer(temp);
}
}
}
}
}
